peaclock
A responsive and customizable clock, timer, and stopwatch for the terminal.
Project Tree
link stdc++fs when using gcc8
Brett Robinson authored 5 years ago
README.md
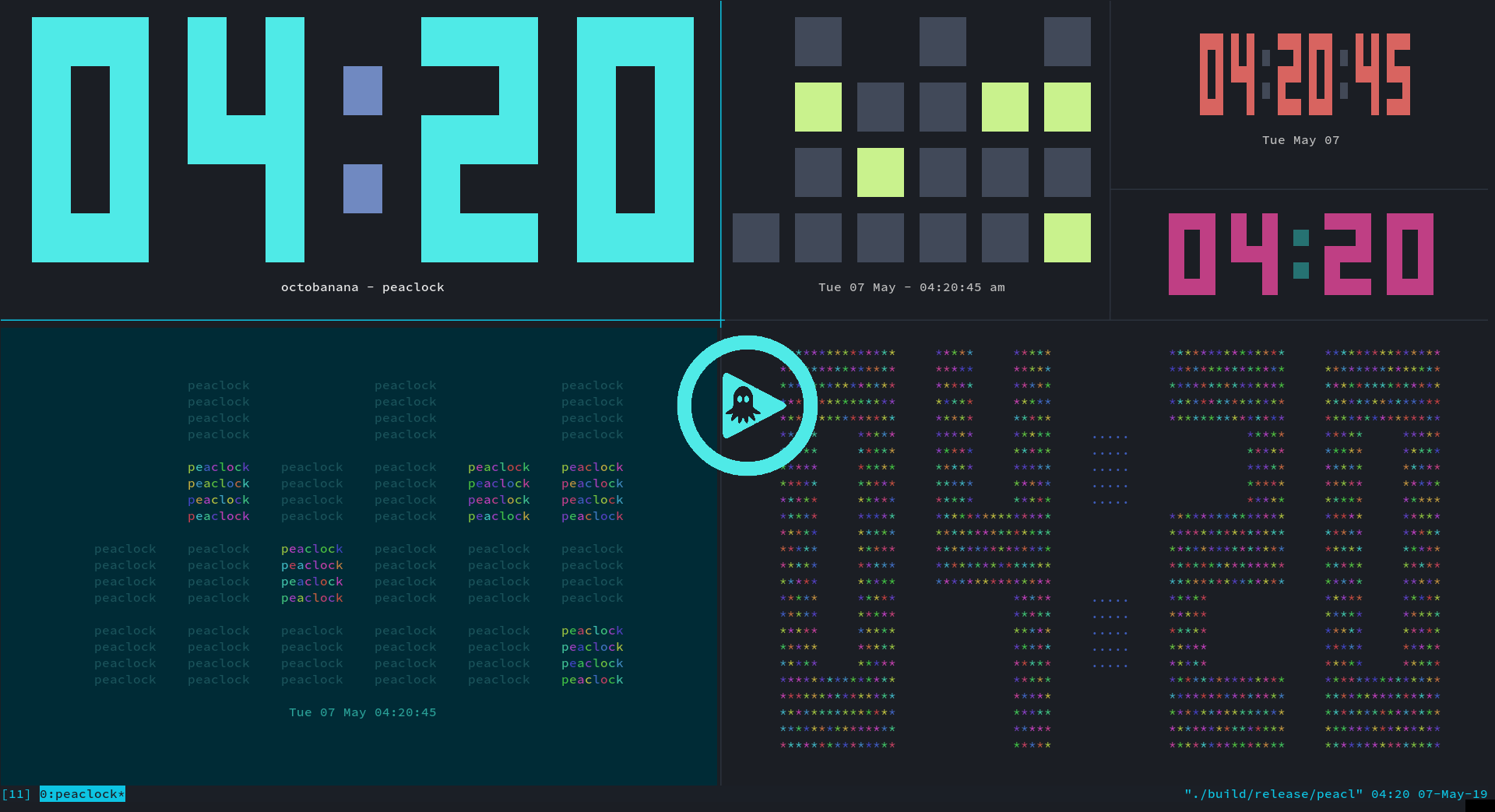
Peaclock
A responsive and customizable clock, timer, and stopwatch for the terminal.
Click the above image to view a video of Peaclock in action.
Contents
About
Peaclock is a responsive and customizable clock, timer, and stopwatch for the terminal.
The clock output changes depending on the selected mode and view. The mode determines the clock value, while the view determines how that value is presented. The clock, timer, and stopwatch modes can be displayed with an ascii, digital, or binary clock view. The clock can be customized, such as changing the width, height, colour, padding, and margin. When in auto size mode, the clock becomes responsive, filling up the full size of the terminal. The clock can also be set to conform to a specific aspect ratio, allowing the clock to auto resize without becoming stretched.
Features
- clock, timer, and stopwatch modes
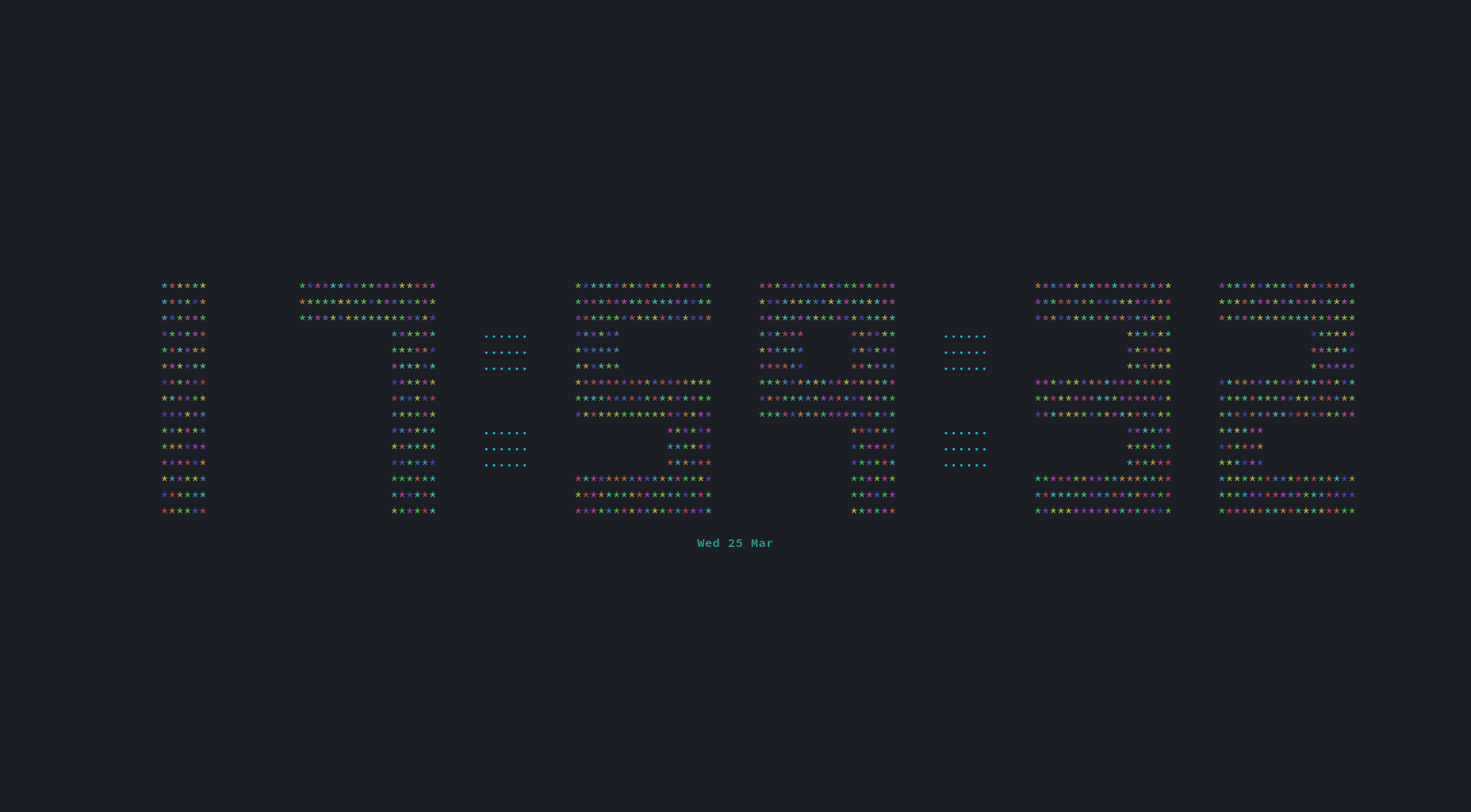
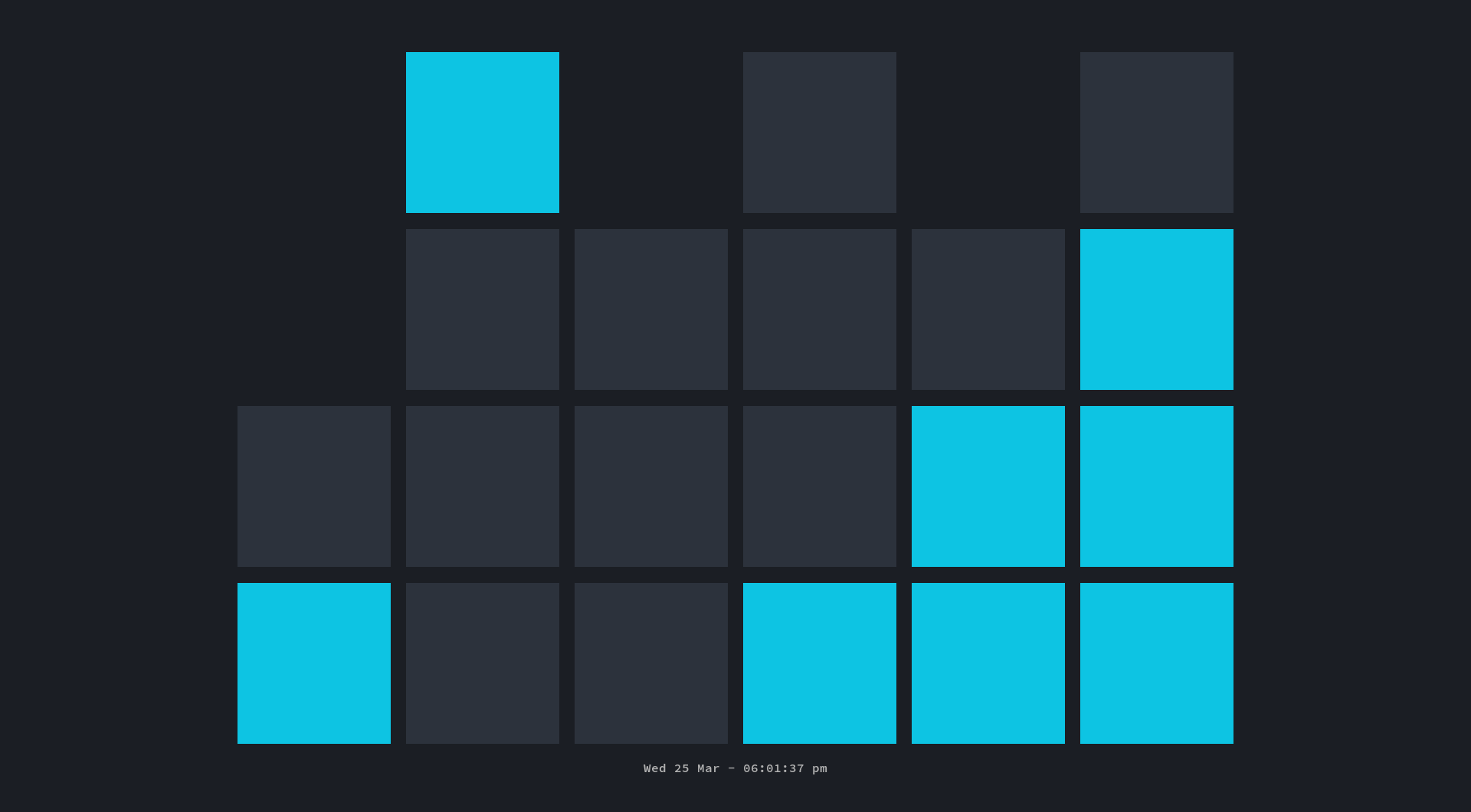
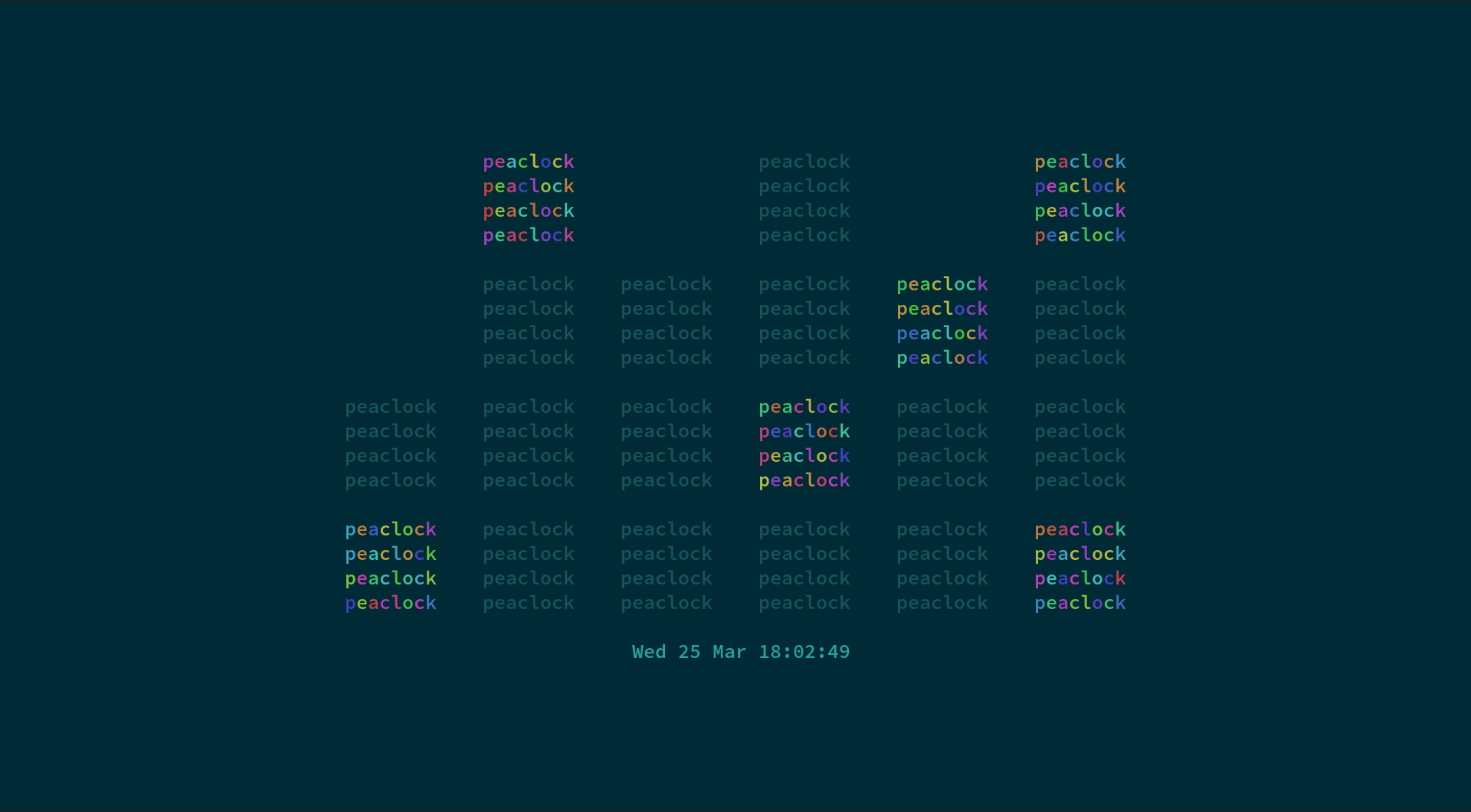
- ascii, digital, and binary clock views
- display a custom date string
- execute a shell command upon timer completion
- set a specific locale
- set a specific timezone
- auto size the clock to fit the width and height of the terminal
- auto size the clock to conform to a specific aspect ratio
- load settings from a configuration file
- save and load the command history
- fuzzy search the command history
- toggle seconds display
- toggle 12 or 24 hour time format
- use 4-bit, 8-bit, and 24-bit colours to personalize the clock
- use the built-in command prompt or a selection of keybindings to adjust and customize the clock while the program is running
Usage
View the usage and help output with the --help or -h flag,
or ./doc/help.txt to view the help output as a plain text file.
Binary Clock
The following is a short guide explaining how to read the binary clock.
| | | < 8
| | | | | < 4
| | | | | | < 2
| | | | | | < 1
H H M M S S < Time Digit
Each column represents a single digit. The first two columns are the two hour digits, the next two are the minute digits, and the last two are the seconds digits.
The bottom row is the low-order bit, which makes it worth a value of 1. The next row up is worth 2, then 4, followed by 8. Adding up the on bits gives the value of the digit.
Terminal Compatibility
This program uses raw terminal control sequences to manipulate the terminal, such as moving the cursor, styling the output text, and clearing the screen. Although some of the control sequences used may not work as intended on all terminals, they should work fine on any modern terminal emulator.
Pre-Build
This section describes what environments this program may run on, any prior requirements or dependencies needed, and any third party libraries used.
Important
Any shell commands using relative paths are expected to be executed in the root directory of this repository.
Environments
- Linux (supported)
- BSD (supported)
- macOS (supported)
Compilers
- GCC >= 8.0.0 (supported)
- Clang >= 7.0.0 (supported)
- Apple Clang >= 11.0.0 (untested)
Dependencies
- CMake >= 3.8
- PThread
- ICU >= 62.1
Linked Libraries
- pthread (libpthread) POSIX threads library
- icuuc (libicuuc) part of the ICU library
- icui18n (libicui18n) part of the ICU library
Included Libraries
- Parg:
for parsing CLI args, modified and included as
./src/ob/parg.hh
macOS
Using a new version of GCC or Clang is required, as the default
Apple Clang compiler does not support C++17 Standard Library features such as std::filesystem.
A new compiler can be installed through a third-party package manager such as Brew. Assuming you have Brew already installed, the following commands should install the latest GCC.
1
2brew install gcc
brew link gccThe following CMake argument will then need to be appended to the end of the line when running the shell script.
Remember to replace the placeholder <path-to-g++> with the canonical path to the new g++ compiler binary.
1./RUNME.sh build -- -DCMAKE_CXX_COMPILER='<path-to-g++>'Build
The included shell script will build the project in release mode using the build subcommand:
1./RUNME.sh buildInstall
The included shell script will install the project in release mode using the install subcommand:
1./RUNME.sh installConfiguration
Config Directory (DIR): ${HOME}/.peaclock
History Directory: DIR/history
Config File: DIR/config
Command History File: DIR/history/command
Use --config=<file> to override the default config file.
Use --config-dir=<dir> to override the default config directory.
The config directory and config file must be created by the user.
The config file in the config directory must be named config.
It is a plain text file that can contain any of the
commands listed in the Commands section of the --help output.
Each command must be on its own line. Lines that begin with the
# character are treated as comments.
If you want to permanently use a different config directory,
such as ~/.config/peaclock, add the following line to your shell profile:
1alias peaclock="peaclock --config-dir ~/.config/peaclock"The following shell commands will create the config directory in the default location and copy over the example config file:
1
2mkdir -pv ~/.peaclock
cp -uv ./cfg/default ~/.peaclock/configSeveral config file examples can be found in the ./cfg directory.
default
octobanana
digital
digital-party
binary
binary-party
binary-unicode
License
This project is licensed under the MIT License.
Copyright (c) 2019 Brett Robinson
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.